배움 저장소
[Data Structures] 챕터9. 이진탐색트리 본문
이진탐색트리
시간복잡도
균형잡힌 트리: O(Log N)
Worst : O(N)
이진 탐색 트리의 한계
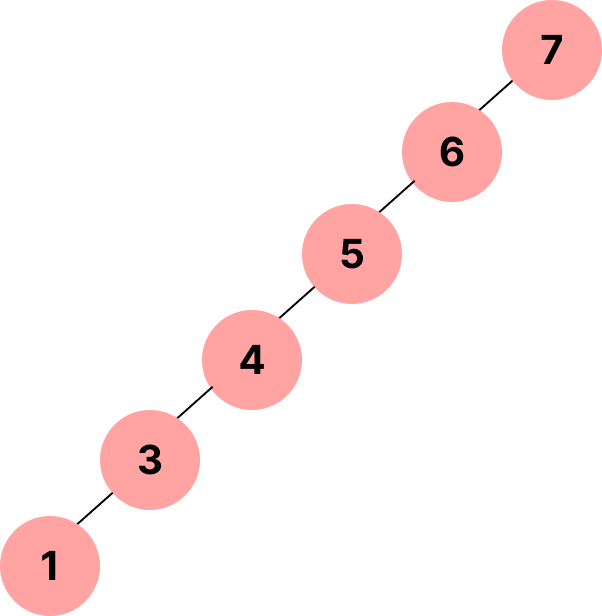
- 완전 이진 트리가 아니므로 비효율적으로 작동할 수 있다
- 역순으로 정렬된 배열 값을 모두 넣을 경우
- 양 서브트리의 깊이가 비슷할 때 효율적이다

구현하기
IterGet
Item* IterGet(const K& key)
{
Node* cur = root_;
while (cur)
{
if (cur->left && key < cur->item.key)
cur = cur->left;
else if (cur->right && cur->item.key < key)
cur = cur->right;
else // handle two case (cur->item == key) & (empty child, No matching)
return &cur->item;
}
return nullptr; // no matching
}
Insert
상위 스택에서 node의 왼쪽 혹은 오른쪽 값을 할당한다.
Node* Insert(Node* node, const Item& item)
{
if (!node)
return new Node{ item, nullptr, nullptr };
if (item.key < node->item.key)
node->left = Insert(node->left, item);
else if (node->item.key < item.key)
node->right = Insert(node->right, item);
else // node->item.key == item.key
node->item = item;
return node;
}
IterInsert
내구현
더보기
void IterInsert(const Item& item)
{
if (!root_) root_ = new Node{ item, nullptr, nullptr };
Node* cur = root_;
while (cur)
{
if (cur->item.key < item.key)
{
if(!cur->right)
{
cur->right = new Node{ item, nullptr, nullptr };
break;
}
cur = cur->right;
}
else if (item.key < cur->item.key)
{
if (!cur->left)
{
cur->left = new Node{ item, nullptr, nullptr };
break;
}
cur = cur->left;
}
else
{
cur->item = item;
break;
}
}
}추천구현
포인터 2개를 사용하면 편하게 부모 값을 저장할 수 있다(포인터 하나 만 쓰려면 반복문 조건으로 손자 노드를 확인해야함)
void IterInsert(const Item& item)
{
if (!root_) root_ = new Node{ item, nullptr, nullptr };
Node* cur = root_;
Node* pre = nullptr;
while (cur)
{
pre = cur;
if (cur->item.key < item.key)
cur = cur->right;
else if (item.key < cur->item.key)
cur = cur->left;
else
{
cur->item = item;
return;
}
}
cur = new Node{ item, nullptr, nullptr };
if(item.key < pre->item.key)
pre->left = cur;
else if(pre->item.key < item.key)
pre->right = cur;
else // it already handled when pre is cur.
assert(false); // pre is cur->right or cur->left
}
Remove
내구현
더보기
Node* Remove(Node* node, const K& key)
{
if (!node) return node;
if (key < node->item.key)
node->left = Remove(node->left, key);
else if (key > node->item.key)
node->right = Remove(node->right, key);
else
{
// case 1. remove node which have two children
if (node->left && node->right)
{
// If right node has a child, take it.
Node* subCurrent = node->right; // subtree's root
if (subCurrent->left)
{
while (subCurrent->left)
{
if (!subCurrent->left->left)
break;
subCurrent = subCurrent->left;
}
Node* child = subCurrent->left;
subCurrent->left = nullptr;
child->left = node->left;
child->right = node->right;
delete node;
return child;
}
else // No left, so return current because it is in-order.
{
subCurrent->left = node->left;
delete node;
return subCurrent;
}
}
// case 2. remove node which had a child (connecting pre and post)
// case 3. remove node which had no child
else
{
// case 3 just assign nullptr to temp
Node* temp = node->left ? node->left : node->right;
delete node;
return temp;
}
}
return node;
}
추천구현
Node* Remove(Node* node, const K& key)
{
if (!node) return node;
if (key < node->item.key)
node->left = Remove(node->left, key);
else if (key > node->item.key)
node->right = Remove(node->right, key);
else
{ // when left is nullptr or right is nullptr or both are nullptr
if (!node->left || !node->right)
{
Node* temp = node->left ? node->left : node->right;
delete node;
return temp;
}
else
{
Node* temp = MinKeyLeft(node->right);
node->item = temp->item; // copy value on target node
// Remove a duplicates on subtree.
node->right = Remove(node->right, temp->item.key);
// "assign value on node->right" handle edge case for
// removed one is just node->right. it return nullptr
}
}
return node;
}
균형잡힌 탐색트리(AVL Tree / Self-Balancing Binary Search Tree)
Balance의 크기 : 왼쪽 자식이 Root인 SubTree의 레벨과 오른쪽 자식이 Root인 SubTree의 레벨 차이
해당 노드 자식간 Balance의 절대값이 2이상일 때 재배열한다.
성능
- AVL 트리는 균형이 맞춰져 있어 삽입, 삭제, 탐색의 평균/최악 시간 복잡도는 O(logN)
- 높이는 매번 새로 계산하거나, 최적화를 위해 Node에 저장해서 값이 바뀔때만 업데이트 한다.
Reference
가시화 도구
- https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
- https://zuramai.github.io/binary-search-tree/
구현방법
- https://www.geeksforgeeks.org/introduction-to-avl-tree/
- https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm
이 때 Left Rotation(왼쪽 위로 끌어올림)에서 B가 왼쪽 자식을 가질 수 있다

이 때 Left Rotation 이전에도 A는 오른쪽 자식을 가지므로 연결관계를 변경해주어 처리하자

Right Rotation(오른쪽 위로 끌어올림)도 위와 같이 처리할 수 있다.
Balance
- 왼쪽 자식의 높이가 높으면 양수, 오른쪽 사직의 높이가 높으면 음수이다
- 자식 Subtree의 높이를 측정한다
int Balance(Node* node)
{
if (node)
return Base::Height(node->left) - Base::Height(node->right);
else
return 0;
}
구현하기
Insert
Node* Insert(Node* node, const Item& item)
{
if (!node)
return new Node{ item, nullptr, nullptr };
const auto& key = item.key;
if (key < node->item.key)
node->left = Insert(node->left, item);
else if (key > node->item.key)
node->right = Insert(node->right, item);
else
{
node->item = item;
return node;
}
// It works recursivly, So below executed after inserting node on child
// It subtract btw child's height
int balance = Balance(node);
// Ref : https://www.geeksforgeeks.org/introduction-to-avl-tree/
// balance가 0, 1, -1 이면 조절할 필요가 없다고 판단
// LL -> Right Rotation
if (balance > 1 && Balance(node->left) >= 0) // node->left->left must exist
node = RotateRight(node); // because blance > 1
// Even if Balance(node->left) == 0 do this because left-left
// RR -> Left Rotation
else if (balance < -1 && Balance(node->right) <= 0) // node->right->right must exist
node = RotateLeft(node); // because blance > 1
// LR -> Left-Right Rotation
else if (balance > 1 && Balance(node->left) < 0)
{
node->left = RotateLeft(node->left);
node = RotateRight(node);
}
// RL -> Right-Left Rotation
else if (balance < -1 && Balance(node->right) > 0)
{
node->right = RotateRight(node->right);
node = RotateLeft(node);
}
return node;
}
Remove
위 Insert 로직을 그대로 가져왔다
Node* Remove(Node* node, const K& key)
{
// BST와 동일
if (!node) return node;
if (key < node->item.key)
node->left = Remove(node->left, key);
else if (key > node->item.key)
node->right = Remove(node->right, key);
else
{
if (!node->left)
{
Node* temp = node->right;
delete node;
return temp;
}
else if (!node->right)
{
Node* temp = node->left;
delete node;
return temp;
}
Node* temp = MinKeyNode(node->right);
node->item = temp->item;
node->right = Remove(node->right, temp->item.key);
}
if (node == NULL)
return node;
// 균형 잡기
int balance = Balance(node);
if (balance > 1 && Balance(node->left) >= 0)
node = RotateRight(node);
else if (balance < -1 && Balance(node->right) <= 0)
node = RotateLeft(node);
else if (balance > 1 && Balance(node->left) < 0)
{
node->left = RotateLeft(node->left);
node = RotateRight(node);
}
else if (balance < -1 && Balance(node->right) > 0)
{
node->right = RotateRight(node->right);
node = RotateLeft(node);
}
return node;
}
영어사전 만들기
구현하기
MyString
#pragma once
#include <iostream>
#include <algorithm> // swap
#include <cassert>
#include <ostream>
class MyString
{
public:
...
bool Validate()
{
for (int i = 0; i < size_; i++)
{
if ('a' <= str_[i] && str_[i] <= 'z'){}
else return false;
}
return true;
}
friend std::ostream& operator << (std::ostream & os, const MyString &Str)
{
for (int i = 0; i < Str.size_; i++)
std::cout << Str.str_[i];
return os;
}
friend bool operator > (const MyString& a, const MyString& b)
{
for (int i = 0; i < std::min(a.Length(), b.Length()); ++i)
if (a.str_[i] != b.str_[i])
return a.str_[i] > b.str_[i];
return a.Length() > b.Length();
}
friend bool operator < (const MyString& a, const MyString& b)
{
for (int i = 0; i < std::min(a.Length(), b.Length()); ++i)
if (a.str_[i] != b.str_[i])
return a.str_[i] < b.str_[i];
return a.Length() < b.Length();
}
friend bool operator <= (const MyString& a, const MyString& b)
{
for (int i = 0; i < std::min(a.Length(), b.Length()); ++i)
if (a.str_[i] != b.str_[i])
return a.str_[i] <= b.str_[i];
return a.Length() <= b.Length();
}
friend bool operator >= (const MyString& a, const MyString& b)
{
for (int i = 0; i < std::min(a.Length(), b.Length()); ++i)
if (a.str_[i] != b.str_[i])
return a.str_[i] >= b.str_[i];
return a.Length() >= b.Length();
}
friend bool operator == (const MyString& a, const MyString& b)
{
if (a.Length() != b.Length())
return false;
for (int i = 0; i < a.Length(); ++i)
if (a.str_[i] != b.str_[i])
return false;
return true;
}
private:
char* str_ = nullptr; // 마지막에 '\0' 없음
int size_ = 0; // 글자 수
};
main.cpp
#include <iostream>
#include <fstream>
#include <string>
#include "MyString.h"
#include "../shared/AVL.h"
using namespace std;
using Item = AVL<MyString, MyString>::Item;
void TestComparison()
{
MyString A = MyString("apple");
MyString B = MyString("board");
MyString C = MyString("cancel");
cout << boolalpha;
cout << (A > B) << endl;
cout << (A < B) << endl;
cout << (A >= B) << endl;
cout << (A <= B) << endl;
cout << (A == B) << endl;
}
void ReadFileAndRichingDictionary(AVL<MyString, MyString> &bst)
{
/* Read Files*/
string temp;
ifstream myfile("eng_dic.txt");
if (myfile.is_open())
{
while (getline(myfile, temp))
{
MyString word{ temp.c_str() };
getline(myfile, temp);
MyString meaning{ temp.c_str() };
if (word.Validate())
{
bst.IterInsert(*(new Item{ word, meaning }));
}
}
myfile.close();
}
else cout << "Unable to open file";
}
int main() {
AVL<MyString, MyString> bst;
// Test
//{
//bst.Insert(Item{ MyString{"aaa"}, MyString{" 1"} });
//bst.Insert(Item{ MyString{"decr"}, MyString{" D"} });
//bst.Insert(Item{ MyString{"cold"}, MyString{" C"} });
//bst.Insert(Item{ MyString{"appl"}, MyString{" A"} });
//bst.Insert(Item{ MyString{"aca"}, MyString{" 3"} });
//bst.Insert(Item{ MyString{"aba"}, MyString{" 2"} });
//bst.Print2D();
//}
// Remove Bugs
//{
// Item *item1 = new Item{ MyString{"abandonment"}, MyString{" 4"} };
// bst.Insert(*item1);
// Item* item2 = new Item{ MyString{"abandonment"}, MyString{" D"} };
// bst.Insert(*item2);
//}
ReadFileAndRichingDictionary(bst);
cout << "Dictionary Created!" << endl;
string temp;
while (std::cin >> temp)
{
auto* Found = bst.IterGet(MyString{ temp.c_str()});
if (Found)
{
cout << "key: " << Found->key << endl;
cout << "\tval: " << Found->value << endl;
}
else
cout << "No result" << endl;
}
return 0;
}
'CS > Data Structure' 카테고리의 다른 글
| [Data Structures] 챕터11. 해슁(Hashing) (0) | 2023.12.22 |
|---|---|
| [Data Structures] 챕터10. 정렬 (0) | 2023.12.22 |
| [Data Structures] 챕터8. 힙 (0) | 2023.12.16 |
| [Data Structures] 챕터7. 트리 (0) | 2023.12.16 |
| [Data Structures] 챕터6. 연결 리스트 (0) | 2023.12.13 |
Comments



